こんにちは!土木ブロガーの監督やっくんです!当ブログへいつも見に来ていただきありがとうございます。いつも本当に感謝してます。
今回は座標計算の求め方についてです。
計算したいけど、計算の仕方が分からないと悩んでいませんか。


平面直角座標系とは
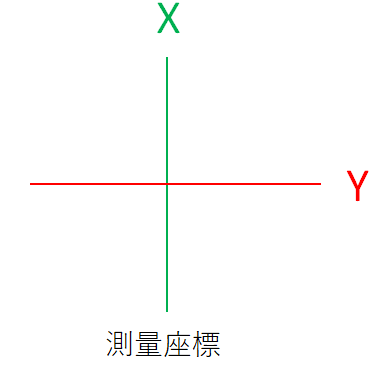
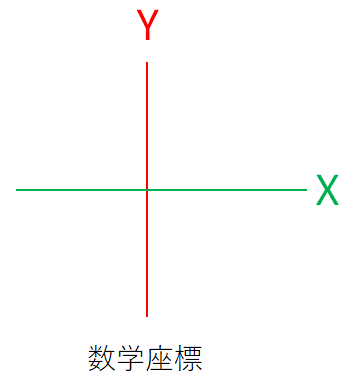
図面を描くうえで、地球を平面に表現するために平面直角座標を使用する。日本国内の公共測量などで使われる座標系。平面直角座標系である測量座標はX軸を縦軸、Y軸を横軸で表す。通常のCADで扱う数学座標とは、X軸とY軸が逆になっている。
座標計算の公式
座標計算に関するポイントは以下の通りです。
座標計算のポイントまとめ
- 座標は(即利用くん)がなくても三角関数で求めることが出来る
- 直角三角形を考えた時に「sin cos tan」を使用する
- 2点の座標値が分かっていれば点間距離と方向角が算出できる
下の公式は覚えましょう!忘れそうな時は携帯などでスクショを撮り、いつでも公式が分かる状態にしましょう!
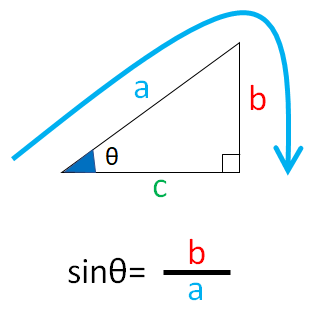
覚えたい公式①
$sinθ=\frac{b}{a}$
筆記体のsを書くイメージ(青色矢印)で覚えましょう!
覚えたい公式②
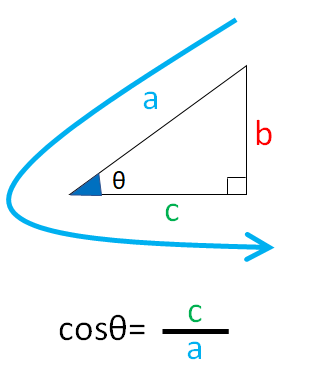
$cosθ=\frac{c}{a}$
cを書くイメージ(青色矢印)で覚えましょう!
覚えたい公式③
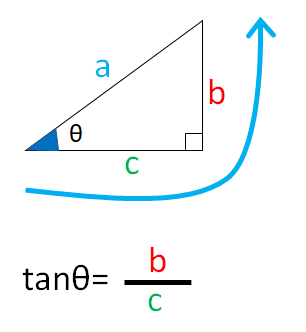
$tanθ=\frac{b}{c}$
筆記体のtを書くイメージ(青色矢印)で覚えましょう!
座標計算の求め方
2点の座標値が器械点A(174.829 207.870)、視準点B(180.201 197.900)を計算する場合
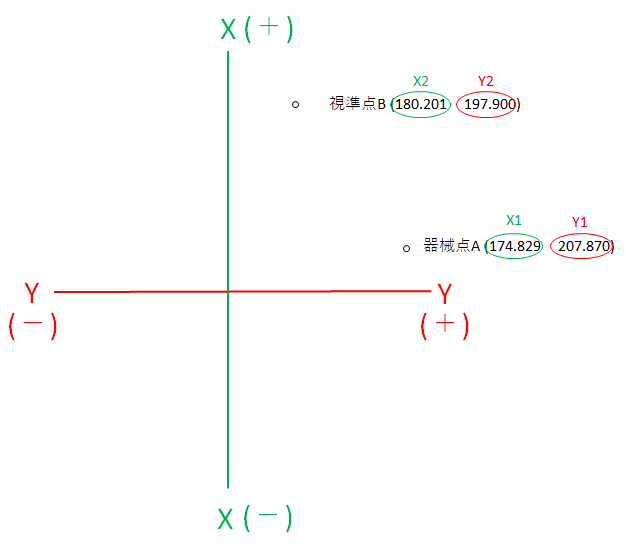
直角三角形を作り、bとcの距離とθの角度を求めてみましょう。
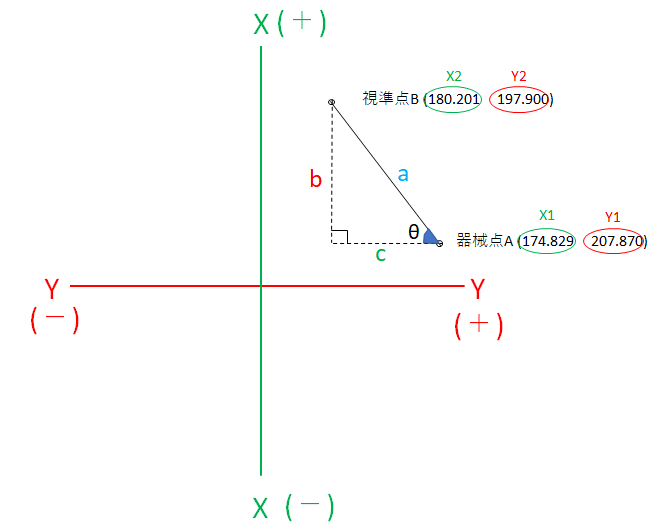
bとcの距離は以下のようになります。
b=X2-X1=5.372
C=Y1-Y2=9.97
次にθを求めてみましょう。
$tanθ=\frac{b}{c}$より
$tanθ=\frac{5.372}{9.97}$
θ=$tan^{-1}(0.53881645)$
θ=28.31651767 ←10進数
θ=28°18′59″ ←60進数
次にaを求めましょう。
aの法長(斜辺の長さ)は三平方の定理を用いて求めることができます。
$a=\sqrt{c^2+b^2}$ $=\sqrt{9.97^2+5.372^2}$=11.325
さらに詳しく
$cosθ=\frac{c}{a}$
上記の公式を使ってもaを求めることができます。
$cosθ=\frac{c}{a}$より
$cos28.31651767=\frac{9.97}{a}$
$a=\frac{9.97}{cos28.31651767}$
$a=\frac{9.97}{0.8803406431}$=11.325
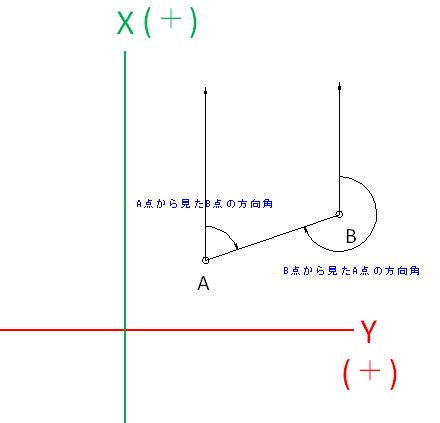
方向角とは
方向角とは、X軸を基準にした時計回りの角度をいいます。
もっとさらに詳しく
θの角度が分かれば方向角を求められる
器械点Aから見た視準点Bの方向角は次のようになります。
方向角は、270度とθを足せば求めることができます。
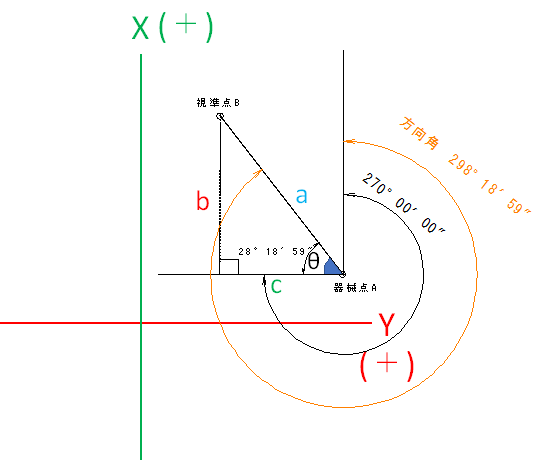
方向角=270°+θ
方向角=270°+28°18′59″=298°18′59″
ココがポイント
以上のことから、2点の座標値が分かれば、点間距離と方向角を求めることができます
まとめ
現場で座標を求める時は、即利用くんを利用したり、座標計算アプリで座標を入力すると計算してくれるソフトはあるが、現場で緊急に計算が必要になった時に計算のやり方が分かると自信に繋がると思います。是非この記事を読んで座標の計算のやり方を覚えましょう!
本ブログでは建設現場でよく使うバーチカルの計算方法とクロソイド曲線の計算についてを紹介しています。以下の記事を本記事と合わせて読んで みてください。
バーチカル計算とクロソイド曲線の計算の仕方が分かるよ~!
【バーチカルの計算方法?】土木工事で使える公式!覚えれば現場で活用できる!
【クロソイド曲線の計算はどんな時に使うの?】計算方法を理解できる!
また座標計算をエクセルで求める方法も紹介しているので読んでみてください!
【座標から距離と方向角を求める方法って?!】エクセルにある数式を入れて計算しよう!
最後まで読んでいただきありがとうございます! 少しでも参考になったと感じていただけたら、応援の為に下記のバナーをクリックしてください!よろしくお願いします。
