こんにちは!土木ブロガーの監督やっくんです!当ブログへいつも見に来ていただきありがとうございます。いつも本当に感謝してます。
今回はクロソイド曲線の計算方法についてです。
計算したいけど、計算の仕方が分からないと悩んでいませんか。


クロソイド曲線(緩和曲線)とは
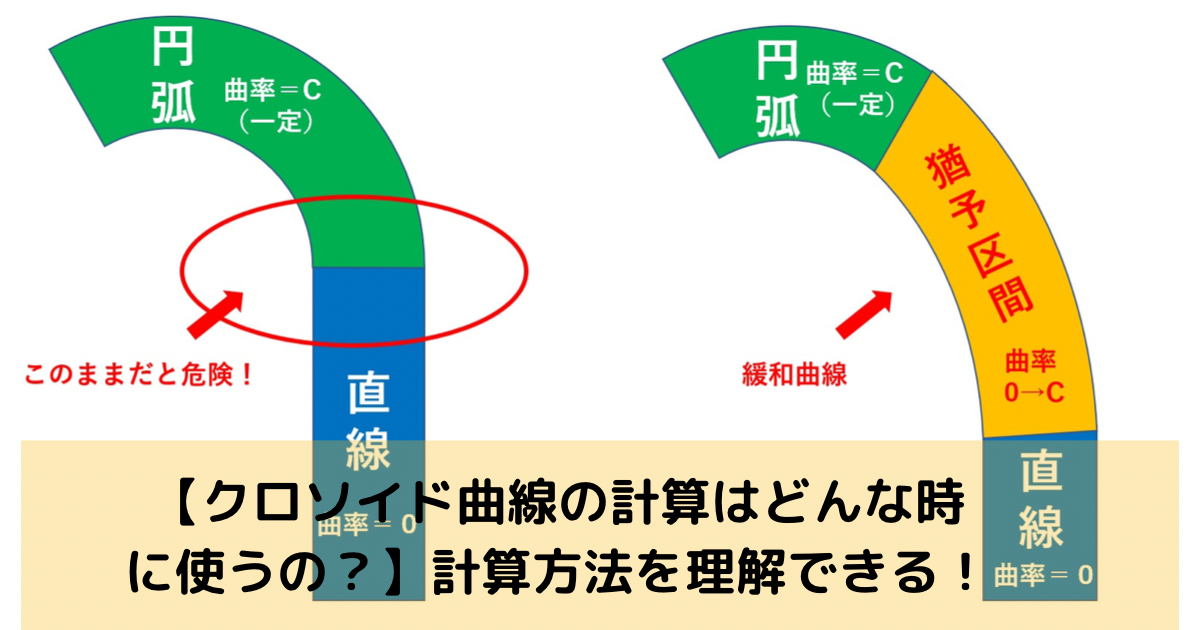
直線からカーブに入る時、いきなりその半径に突入しないで直線(半径無限大)から徐々に半径を小さくしていく曲線です。
例えば、高速道路を運転しているドライバーにとってカーブを曲がる時に急ハンドルとなる道路形状は事故に繋がり大変危険。その為、高速道路のインターチェンジやジャンクションなどのように、ある程度速いスピードで保ったまま曲がる場所では、なるべくスムーズなハンドル操作でカーブを曲がることが出来るように緩和曲線が利用されている。
クロソイド曲線が入ったカーブの曲率図を描いてみましょう。クロソイド曲線では、距離に応じて曲率が一定の割合で増加するので、カーブ全体の曲率は下のようになります。
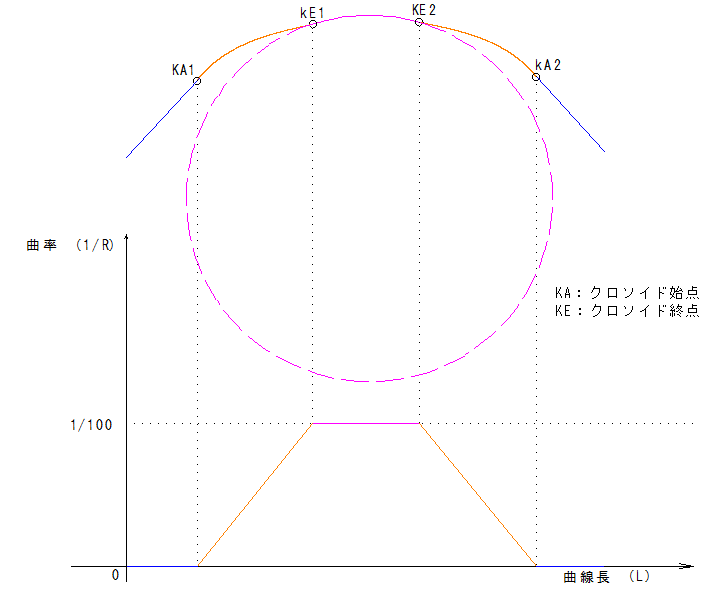
オレンジ色の部分がクロソイド曲線です。この長さの分だけ、ハンドルを回す距離(時間)が与えられるので、単曲線に比べ、スムーズに車が曲がっていくことができます。
クロソイドの基本式
クロソイド曲線に関するポイントは次の通りです。
クロソイド曲線のポイントまとめ
- Aはパラメータと呼ばれ、クロソイド曲線の曲率の増加度を表し、車のハンドルを回すスピードを表している
- クロソイド曲線はR(半径)、L(クロソイド区間の長さ)、A(パラメータ)のいずれか2つの要素により、形が決定することができる
下の計算式は覚えましょう!忘れそうな時は携帯などでスクショを撮り、いつでも分かる状態にしましょう!
この計算式は覚えよう!
$A^2=R×L$ $L=\frac{A^2}{R}$
(A、L、R、は設計図書の平面図、縦断図に記載されています)
A:クロソイドパラメータ
L:クロソイド曲線長
R:曲率半径
KA:クロソイド始点
KE:クロソイド終点
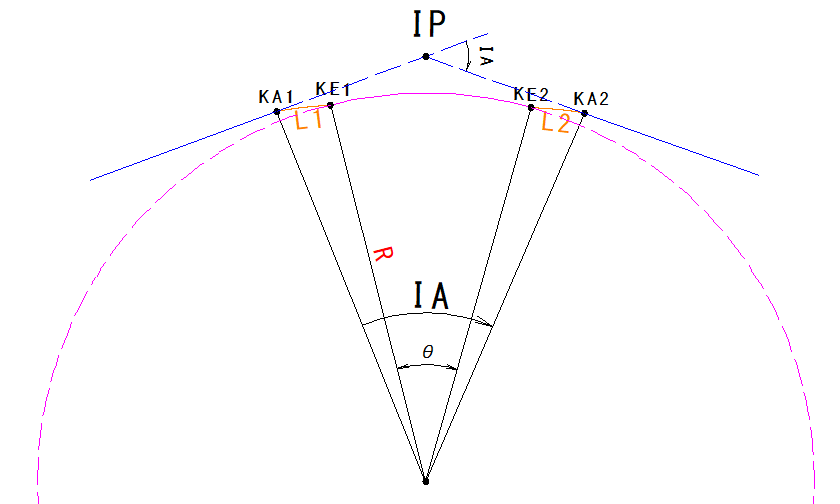
クロソイド曲線の求め方
点KA1から点KA2の路線長を求めるには、クロソイド曲線長L1とL2を求めてCLの単心曲線を合計すれば求められます。
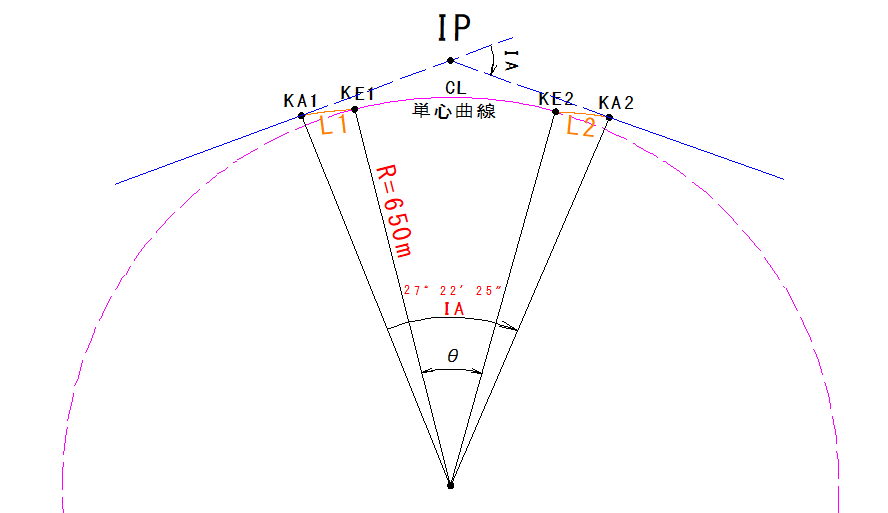
まず最初にクロソイド曲線長L1とL2を求めてみましょう。
クロソイドパラメータは170m、円曲線の曲線半径はR=650m、クロソイド曲線の交角IA=27°22′25″、円周率はπ=3.142とする。
$L1=\frac{A^2}{R}$ $=\frac{170^2}{650}$ = 44.462mとなり
KA1~KE1のL1とKE2~KA2のL2=44.462mとなります。
次にKE1~KE2の単心曲線のCLを求めましょう。
さらに詳しく
$θ=IA-\frac{180°L}{πR}$
まずは、CLを求めるためにはθを求める必要があるので、上記の計算式を使ってθを求めます。
$θ=IA-\frac{180°L}{πR}$
$=27°22′25″-\frac{180°×44.462}{3.142×650}$
=27°22′25″-3°55′7.32″
=23°27′17.68″となります。
もっとさらに詳しく
$CL=2Rπ×\frac{θ}{360°}$
上記の計算式を使ってCLを求めましょう。
$CL=2Rπ×\frac{θ}{360°}$
$=2×650×3.142×\frac{23°27′17.68″}{360°}$
=266.122mとなります。
よって点KA1から点KA2の路線長は
KA1~KA2=L1+CL+L2
=44.462+266.122+44.462
=355.046mとなります。
このように、上の計算式を覚えておけば平面図や縦断図にパラメータ、クロソイド曲線、半径が記載されていない場合や不明な時に、この計算式を使えば求められます!
まとめ
クロソイド曲線の計算は、クロソイド曲線(要素計算)等で出来ますが、技術者として計算の方法や計算の理屈を理解することは重要です。「何故この計算はこうなるのか?」と思うことは大切なことで、今回解説した計算方法が分かれば、現場での変更やトラブルにもきっと対応できるでしょう。
【バーチカルの計算方法?】土木工事で使える公式!覚えれば現場で活用できる!
クロソイド曲線についてより詳しく勉強したい方は是非↓
最後まで読んでいただきありがとうございます! 少しでも参考になったと感じていただけたら、応援の為に下記のバナーをクリックしてください!よろしくお願いします。
